Materi Matematika Minat : Logaritma

Materi Matematika Minat : Logaritma

Add Comment Edit



Definisi dan Sifat-Sifat Logaritma

Hasil gambar untuk math aesthetic

Pembahasan pertama dalam materi logaritma adalah definisi dan sifat-sifat logaritma. Melalui sifat-sifat logaritma yang akan kita bahas nanti, sobat idSCHOOL pasti akan bisa menyelesaikan semua variasi soal logaritma. Fungsi logaritma merupakan kebalilkan (invers) dari fungsi eksponen atau perpangkatan. Secara umum, bentuk logaritma dinyatakan dalam bentuk berikut.
definisi dan sifat-sifat logaritma

Contoh menghitung nilai logaritma
  \[^{2}\textrm{log } 8 \textrm{ = ....}\]
Untuk menyelsaikan nilai logaritma di atas, kita perlu mencari tahu nilai berapa yang tepat untuk mengganti x pada persamaan 2x = 8. Nilai yang tepat untuk mengganti nilai x adalah 3 karena 23 = 8.
Jadi, nilai 2log 8 = 3.
Contoh nilai logaritma lainnya adalah sebagai berikut
3log 27 = 3 karena 33=27
3log 243 = 5 karena 35=243
4log 16 = 2 karena 42=16
5log 125 = 3 karena 53=125
10log 100 = 2 karena 102=100

Sifat-Sifat Logaritma

Kunci sukses untuk menyelesaikan soal-soal logaritma yang lebih rumit adalah memahami dan menguasai sifat-sifat logaritma seperti berikut.
  \[^{\textrm{a}}\textrm{log bc = }^{\textrm{a}}\textrm{log b + }^{\textrm{a}}\textrm{log c}\]
  \[^{a}\textrm{log }\frac{b}{c}\textrm{ = }^{a}\textrm{log b }-\textrm{ }^{a}\textrm{log c}\]
  \[^{\textrm{a}}\textrm{log b}^{\textrm{n}}\textrm{ = n}\cdot^{\textrm{ a}}\textrm{log b}\]
  \[^{a}\textrm{log b}^{n}\textrm{ = }\frac{n}{m}\textrm{.}^{a}\textrm{log b}\]
  \[^{a}\textrm{log b = }\frac{\textrm{log b}}{\textrm{log a}}\textrm{ = }\frac{1}{^{b}\textrm{log a}}\]
  \[^{\textrm{a}}\textrm{log b } \cdot ^{\textrm{ b}}\textrm{log c = } ^{\textrm{a}}\textrm{log c}\]
  \[\textrm{a}^{^{\textrm{a}}\textrm{log b}}\textrm{= b}\]
  \[^{\textrm{a}}\textrm{log a = 1}\]
  \[^{\textrm{a}}\textrm{log 1 = 0}\]

Grafik Logaritma

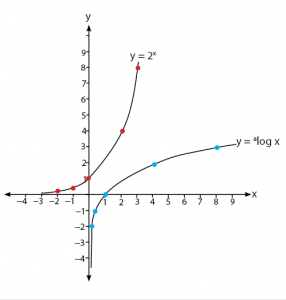
Fungsi logaritma yang dinyatakan dalam y = ^{a}log \;x dapat digunakan untuk membantu menentukan grafik fungsi logaritma. Gambar di bawah adalah grafik logaritma beserta inversnya.

Contoh Soal dan Pembahasan

Berikut adalah contoh-contoh soal yang menggunakan definisi dan sifat-sifat logaritma.
Contoh 1
Nilai dari
  \[ \frac{^{5}\textrm{log 3.}^{9}\textrm{log 125 + }^{5}\textrm{log 625}}{^{3}\textrm{log 81}-^{3}\textrm{log 9}}\]
adalah = …. (Soal UN Matematika SMA 2016)
  \[\textrm{A. }\frac{121}{4}\]
  \[\textrm{B. }\frac{111}{4}\]
  \[\textrm{C. }\frac{121}{16}\]
  \[\textrm{D. }\frac{81}{16}\]
  \[\textrm{E. }\frac{11}{4}\]
Pembahasan:
  \[\frac{^{5}\textrm{log 3.}^{9}\textrm{log 125 + }^{5}\textrm{log 625}}{^{3}\textrm{log 81}-^{3}\textrm{log 9}}\textrm{ = }\frac{^{5}\textrm{log 3.}^{3^{2}}\textrm{log 5}^{3} \textrm{ + } ^{5}\textrm{log 5}^{4}}{^{3}\textrm{log }\frac{81}{9}}\]
  \[\textrm{ = }\frac{^{5}\textrm{log 3.}\frac{3}{2}^{3}\textrm{log 5}\textrm{ + } 4^{5}\textrm{log 5}}{^{3}\textrm{log 9}}\]
  \[\textrm{ = }\frac{\frac{3}{2}^{5}\textrm{log 3.}^{3}\textrm{log 5}\textrm{ + } 4^{5}\textrm{log 5}}{^{3}\textrm{log 3}^{2}}\]
  \[\textrm{ = }\frac{\frac{3}{2}^{5}\textrm{log 5}\textrm{ + } 4^{5}\textrm{log 5}}{2^{3}\textrm{log 3}} \]
  \[ \textrm{ = }\frac{\frac{3}{2}\textrm{(1)}\textrm{ + } 4\textrm{(1)}}{2\textrm{(1)}} \]
  \[ \textrm{ = }\frac{\frac{3}{2}\textrm{ + }\frac{4}{2}}{2} \]
  \[ \textrm{ = }\frac{\frac{11}{2}}{2} \]
  \[ \textrm{ = }\frac{11}{4} \]
Jawaban: E

Contoh 2
Jika 2log 3 = a dan 3log 5 = b maka 5 log 20 = ….
  \[ \textrm{A. }\frac{2}{a} \]
  \[ \textrm{B. }\frac{2+ab}{a(1+b)} \]
  \[ \textrm{C. }\frac{a}{2} \]
  \[ \textrm{D. }\frac{b+1}{2ab+1} \]
  \[ \textrm{E. }\frac{a(1+b)}{2+ab} \]
Pembahasan:
  \[ ^{15}\textrm{log 20}=\frac{^{3}\textrm{log 20}}{^{3}\textrm{log 15}} \]
  \[ =\frac{^{3}\textrm{log (2}^{2}.5)}{^{3}\textrm{log (3.5)}} \]
  \[ =\frac{^{3}\textrm{log 2}^{2}+^{3}\textrm{log 5}}{^{3}\textrm{log 3}+^{3}\textrm{log 5}} \]
  \[ =\frac{2^{3}\textrm{log 2}+^{3}\textrm{log 5}}{^{3}\textrm{log 3}+^{3}\textrm{log 5}} \]
  \[ =\frac{2\frac{1}{^{2}\textrm{log 3}}+^{3}\textrm{log 5}}{^{3}\textrm{log 3}+^{3}\textrm{log 5}} \]
Substitusi nilai 2log 3 = a dab 3 pada persamaan di atas sehingga diperoleh persamaan berikut.
  \[ =\frac{2\frac{1}{a}+b}{1+b}=\frac{\frac{2}{a}+b}{1+b}=\frac{\frac{2+ab}{a}}{1+b}=\frac{2+ab}{a(1+b)} \]
Jawaban: C
Demikianlah tadi definisi logaritma dan sifat-sifat logaritma. Mudah kan? Masih ada pertanyaan? Tinggalkan komentar di bawah! Terimakasih sudah mengunjungi idschool(dot)net, semoga bermanfaat!

Share this:

ABOUT THE AUTHOR

Hello everyone! My name is Hana. Wekcome to my blog!

0 comments:

Post a Comment

Subscribe to: Post Comments ( Atom )